基于物理的渲染:基于图像照明(Image-based Lighting)
基于图像的照明(Image-based Lighting)在基于物理的渲染方法之中,如果想获得非常好的渲染效果,则需要分析光线的传播来进行全局光照(直接光照与间接光照)的计算,但该方法所需要的计算代价是巨大的,“往往”无法支持实时的需要。相反,如果仅仅考虑光源的直接光照,虽然渲染速度提升,但是渲染质量却不尽如人意,而基于图像照明(IBL)就是这样一种处于两个“极端”之间的方法,把天空盒环境贴图上的颜色信息当做环境光源,通过对反射方程的近似计算,从而生成采样贴图,最终计算光照能量时仅仅需要去对这个贴图进行采样再加以计算即可,相比于完整的全局光照减轻了计算代价,同时也带来了不错的渲染质量的提升,以下本文便会详细介绍这样一种渲染技术。 1 预备知识(在第一章中回顾一些简略的基础知识,详细讲解可以查看我的前几篇笔记) 根据learnopengl中定义,一般把满足如下三个条件的渲染称为基于物理的渲染: 1.基于微平面理论 2.使用基于物理的BRDF 3.保证能量守恒 1.1 微平面理论所谓微平面理论(Microfacets Theory),就是从微观的角度去观察物体,并认为物体的表面在到达微观的尺度之后,都是由许许多多的更小的理想镜面所组成的。 当这些微小的理想镜面的法线方向较为集中一致的时候,从宏观角度来看,物体的镜面反射会比较明显,反之,当这些微小镜面的法线方向较为杂乱的时候,物体表面则会相对粗糙。如下图所示: 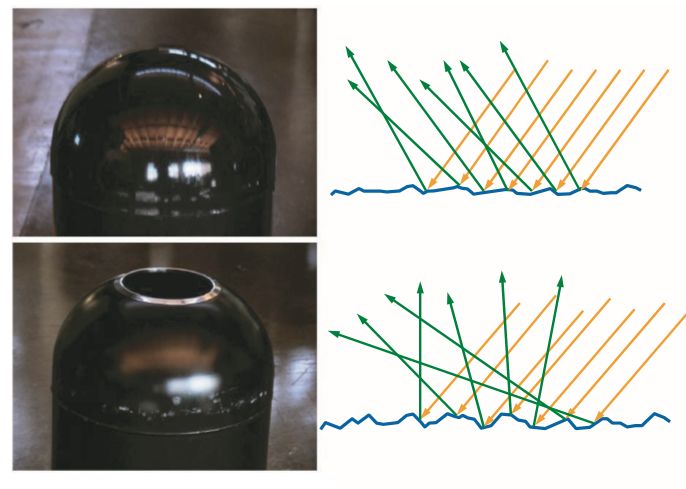 (可以看到,第一幅图的微平面的镜面法线方向比较集中,第二幅图中的微平面的镜面法线方向比较分散) 当然并不是所有的光都会被微表面直接反射的。当光线照射到物体表面时,一部分光线会与表面的许许多多的微小镜面发生镜面反射,另一部分光线则会折射进入物体内部,如下图: 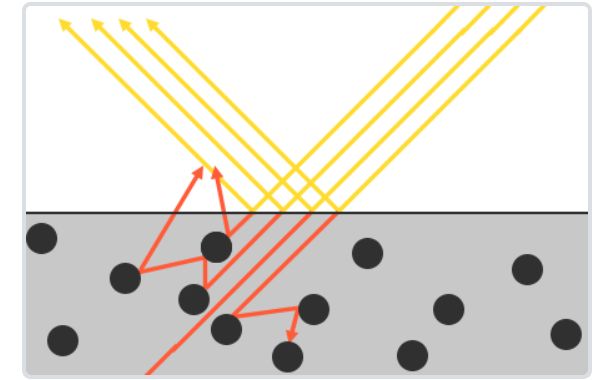 当光线折射进入内部的时,会与物体的微小粒子不断发生碰撞并散射到随机方向,在碰撞的过程中一部分光线会被吸收转换为热能,还有一部分光线会因为散射方向的随机性重新离开表面,而这部分光线就恰好形成了漫反射。 1.2 反射方程与BRDF具体来说,上述所讲的微平面理论会体现在反射方程当中的BRDF中。 首先回顾一下反射方程: 其中 正如一开始所说,对于基于物理与微平面理论的特点,就体现在BRDF之上,一般使用的微平面模型为Cook-Torrance模型,其BRDF为: 其中: 1.2.1 菲涅尔项 F其中: 1.2.2 法线分布函数 DD是法线分布函数,衡量微平面法线的分布情况,物理含义为每单位面积,每单位立体角下所有法向为 其中: 1.2.3 几何遮挡函数 GG是几何函数,为了表示微平面的自遮挡从而引起的光线损失,如下图所示:  左边一幅图中是入射光线无法照射到一些微平面,这种情况称为Shadowing,右边图中是反射光线无法正常到达人眼,称为Masking,而几何函数G正是为了模拟出这两种情况所导致的光线损失,在UE4中采用了Schlick-GGX来进行建模: 其中: (注:这里仅仅使用IBL作为光源) 2 基于图像的照明 IBL不如想象这样一个场景:所有需要渲染的模型都处于一个巨大的球体的中心,球体上的每一个点都会发出光线照射模型,因为球体的相对"巨大",所以模型之上的相对移动都可以忽略,因此对于模型上的每一点能接收到来自球体的光线都由其法线所在半球决定,如下图所示: 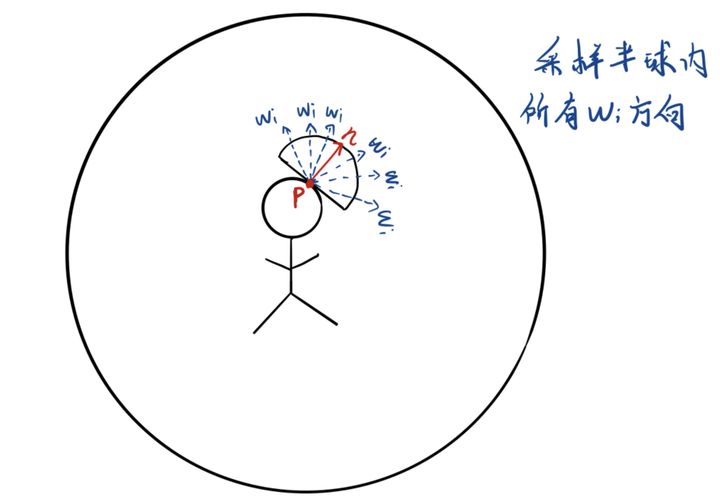 对于一个如下图这样的天空盒只需要给定采样方向就可以获得入射光的辐射度: (天空盒与球体是互通的)  采样结果: 以上正是基于图像的照明的想法,正如开篇所讲其实就是利用了整个天空盒贴图来当作光源,以更多的环境光源来提升渲染的质量,这里的难点就是,如果我们每算一个点都要去用该点法线所在半球的所有方向来采样天空盒,获得辐射度结果,来充当反射方程的入射光 2.1 漫反射部分将第一章提到的Cook-Torrance BRDF 带入反射方程得到: 进一步,将反射方程展开: 其中左半部分即为漫反射部分,右半部分即为镜面反射部分,首先考虑漫反射部分,同时将 其中 与原始式子相比有两个区别: 1.第一个括号的 2.第二个括号的 现在漫反射项的积分值仅仅取决于法线向量 对于积分的计算可以直接使用蒙特卡洛积分的方法,在 将 只要遍历所有法线方向,再利用上式计算出每个法线向量所对应的结果,存储在贴图中即可,称该贴图为irradiance map。同样不难想象,因为遍历了所有法线方向,存储下来的贴图依然是一个6张的天空盒贴图:  当然最终实际渲染的时候,也是利用法线 2.2 镜面反射部分根据反射方程,镜面反射部分如下: 其中: 此时的积分值会因为 2.2.1 prefilter environment map(以下推导证明,很大程度参考了 仔细观察近似之后式子的右半部分,不难发现其实是一个蒙特卡洛积分的形式,我们将其还原: 如此,不难进一步推导出,对于分解之后左边括号的内容其实是对这样一个式子的近似: 以下我们暂且把右边部分放在一旁,首先解释分解的左边部分。利用蒙特卡洛积分的方法,将分子和分母分别展开: 将 接下来对概率密度函数 其中 而我们都知道的一点是,pdf在其整个积分域的积分值为1,所以该积分式中的被积项 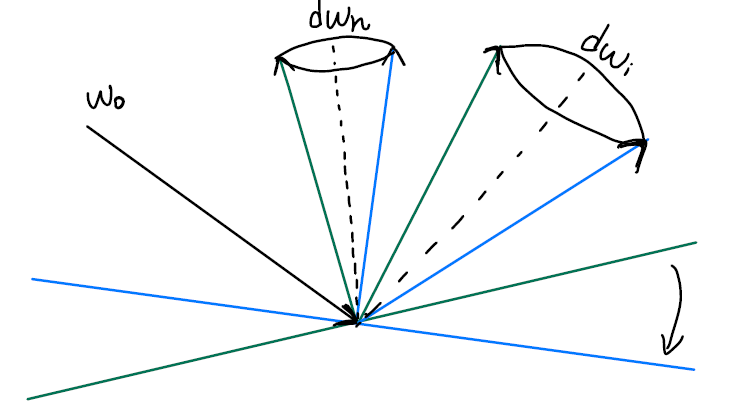 首先固定观察方向  根据图中的单位球面坐标系以及标注的角度,不难得出 同时 此时已经知道了 将其带入 因此,最终得到 出于以下两点考虑,约去分子分母的菲涅尔项的 1.当物体表面比较光滑时,采样的 2.当物体表面比较粗糙时,最终的radiance计算结果也会比较粗略,加不加 虚幻4在此之上做了进一步的假设,即令 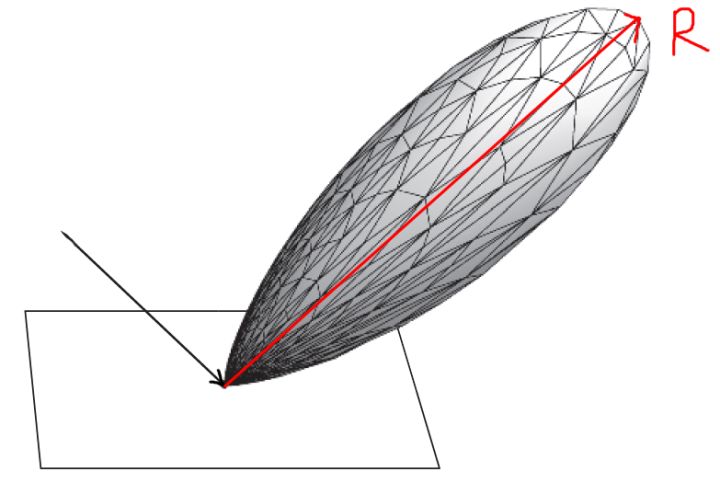 在不同方向入射时(除掠角),波瓣的变化不大,所以会有: 转变示意图: 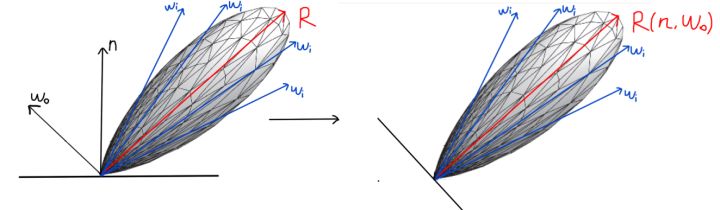 (注意这里的 将假设条件带入原积分式子得: 其中进一步化简: 呼~! 经过一众的近似化简推导之后,我们终于得到了与虚幻4所给出的分解十分相似的结果,不过害有一点不一样的是,虚幻4中用 由于假设了  需要注意的是这里与irradiance map不同的是需要使用反射方向 2.2.2 BRDF LUT再观察这个分解的式子: 此时积分中含有的变量为: 推导的最后一步已经成功的将积分内的 将2.2.1节所推导得到的 同样不难推导出B: 计算得到的贴图称为LUT,如下: 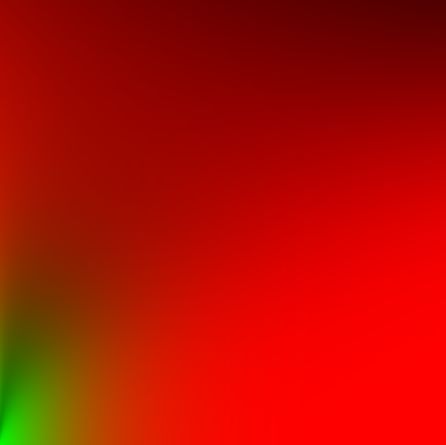 附上lut计算代码: 最后在真正渲染时,计算某个点着色的过程只需要对贴图采样再加以计算即可: fragment_shader伪代码: 3 总结以上就是IBL的所有过程了,不难看出为了得到实时的效果,在计算镜面反射项的时候进行了大量的近似,误差主要来源就是这里,但利用IBL对渲染效果提升是巨大的,可以看几张渲染图:   最后再贴一下我自己写的软光栅渲染器: 简单的Blinn-Phong模型与IBL都有实现。包括一些其它的图形学基础算法,这里就不在列举了。 主要特点是纯C++实现,没有任何依赖,核心代码大概在2000多行,因此比较适合阅读与学习,如果有任何错误与问题也欢迎指正交流!  Reference[1]Ubp.a:深入理解 PBR/基于图像照明 (IBL) [2]moriya苏蛙可:DX12渲染管线(1) - 基于物理的渲染(PBR) [3] LearnOpenGL [4] Real shading in Unreal Engine 4 [5] Background: Physics and Math of Shading by Naty Hoffmann |
最新评论
 |手机版|小黑屋|九艺游戏动画论坛
( 津ICP备2022000452号-1 )
|手机版|小黑屋|九艺游戏动画论坛
( 津ICP备2022000452号-1 )
GMT+8, 2024-7-27 12:15 , Processed in 0.048510 second(s), 18 queries .
Powered by Discuz! X3.4 © 2001-2017 Discuz Team.






